Hình lăng trụ đứng là một hình khối thường gặp trong đời sống và toán học. Bạn đã biết rõ về khái niệm cũng như công thức tính hình khối này chưa? Cùng theo dõi bài viết để biết cách tính diện tích xung quanh, toàn phần hình lăng trụ đứng và các ví dụ chi tiết nhé!
Mục lục bài viết
Khái niệm hình lăng trụ đứng
Khái niệm: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.
Tính chất
– Hình lăng trụ đứng có tất cả cạnh bên vuông góc với hai đáy.
– Hình lăng trụ đứng có tất cả mặt bên là các hình chữ nhật.
Diện tích hình lăng trụ đứng
Cách tính diện tích xung quanh hình lăng trụ đứng
Ý nghĩa: Diện tích xung quanh hình lăng trụ đứng là tổng hiện tích các mặt bên của hình lăng trụ đứng.
Diện tích xung quanh hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao.
Công thức: Sxq = p.h
Trong đó:
+ p là chu vi đáy.
+ h là chiều cao.
.jpg)
Sau đây mình sẽ hướng dẫn các bạn cách tính diện tích xung quanh hình lăng trụ đứng thông qua ví dụ sau.
Ví dụ: Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích xung quanh của hình lăng trụ đứng là?
Hướng dẫn giải:
– Chu vi đáy hình chữ nhật ABCD= 2(AB + BC)= 2(4 + 5) = 18 (cm).
– Diện tích xung quanh hình lăng trụ đứng ABCD.A’B’C’D’ = p.h = 18.2,5= 45 (cm2).
Cách tính diện tích toàn phần hình lăng trụ đứng
Ý nghĩa: Diện tích toàn phần của hình lăng trụ đứng là tổng diện tích xung quanh và diện tích hai đáy.
Diện tích toàn phần của hình lăng trụ bằng tổng các diện tích xung quanh và diện tích hai đáy.
Công thức: Stp = Sxq + 2S
Trong đó:
– Sxq là diện tích xung quanh.
– S là diện tích đáy.
.jpg)
Sau đây mình sẽ hướng dẫn các bạn tính diện tích toàn phần hình lăng trụ đứng thông qua ví dụ sau.
Ví dụ: Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 4cm BC = 5cm, chiều cao h = 2,5cm. Diện tích toàn phần của hình lăng trụ đứng là?
Hướng dẫn giải:
– Diện tích xung quanh hình lăng trụ đứng ABCD.A’B’C’D’ = p.h = (2(AB + BC)) . 2,5 = 45 (cm2).
– Diện tích đáy hình chữ nhật ABCD = 4.5 = 20 (cm2).
– Diện tích toàn phần hình lăng trụ đứng ABCD.A’B’C’D’ = Sxq + 2.S = 45 + 2.20 = 85 (cm2).
Thể tích hình lăng trụ đứng
Ý nghĩa: Thể tích hình lăng trụ đứng là lượng không gian mà vật ấy chiếm.
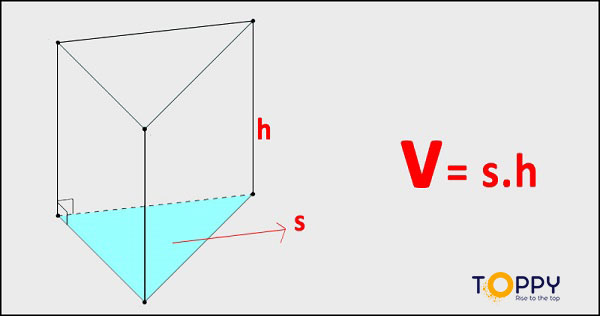
Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.
Công thức: V = S. h
Trong đó:
– S: diện tích đáy.
– h: chiều cao.
.jpg)
Sau đây mình sẽ hướng dẫn các bạn tính thể tích hình lăng trụ đứng thông qua ví dụ sau.
Ví dụ: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Hình lăng trụ có chiều cao h = 5cm. Thể tích của hình lăng trụ đó là?
Hướng dẫn giải:
– Diên tích đáy là tam giác ABC = ½.AB.AC= ½ .3.4 = 6 (cm2).
– Thể tích hình lăng trụ đứng ABC.A’B’C’= SABC.h = 6.5 = 30 (cm3).
Các dạng bài tập của hình lăng trụ đứng:
1. Dạng 1: Xác định các mối quan hệ giữa góc, cạnh và mặt phẳng.
Để có thể xử lý được dạng bài tập về việc xác định các mối quan hệ giữa góc, cạnh và mặt phẳng đối với hình lăng trụ này cần áp dụng tính chất của chúng. Bên cạnh đó là sử dụng mối quan hệ vuông góc hoặc song song giữa mặt phẳng với mặt phẳng, đường thẳng với mặt phẳng, đường thẳng với đường thẳng để có thể giải thích cũng như chứng minh được dạng này.
2. Dạng 2: Tính diện tích, độ dài và thể tích hình lăng trụ đứng.
Hình lăng trụ dạng đứng là hình có các tính chất đặc biệt khác với những hình lăng trụ thông thường khác. Chính vì vậy mà công thức tính diện tích, độ dài và thể tích hình lăng trụ đứng cũng phụ thuộc vào những tính chất riêng biệt này. Để có thể xử lý được dạng bài tập này cần áp dụng công thức đã cho như ở trên để xác định được độ dài, thể tích của hình lăng trụ đứng, diện tích xung quanh và diện tích toàn phần,…
Dạng bài tập tính diện tích, độ dài và thể tích
Bài giảng trên đã tổng hợp những kiến thức lý thuyết về hình lăng trụ đứng cũng như các dạng bài tập thông dụng về diện tích và thể tích hình. Hy vọng đây sẽ là những tài liệu và kiến thức bổ ích dành cho các em học sinh. Việc học thật chắc kiến thức cơ bản và sau đó vận dụng vào bài tập là điều cần thiết. Các em hãy thường xuyên ôn luyện để giải các dạng bài tập này nhanh hơn và đúng hơn, giúp ích cho các kỳ thi nhé.


